Le microscope numérique
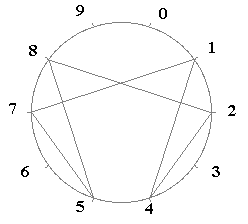
Voici le graphe de 1/7 en base 10 :
1/7 est égal à 0,142857142857...où la période 142857 se répète indéfiniment.
Rapportons les chiffres de 0 à 9 (utilisés dans le calcul en base 10) autour d'un cercle, et relions-les dans l'ordre imposé par la période.
Cette période est 142857:

Une constatation s'impose d'elle-même :
Cette période est unique pour toutes les fractions de 1/7 en base 10.
1 x 142857 = 142857 et 1/7 = 0,142857...
2 x 142857 = 285714 et 2/7 = 0,285714...
3 x 142857 = 428571 et 3/7 = 0,428571...
4 x 142857 = 571428 et 4/7 = 0,571428...
5 x 142857 = 714285 et 5/7 = 0,714285...
6 x 142857 = 857142 et 6/7 = 0,857142...
7 x 142857 = 999999 et 7/7 = 0,999999...
Ici se trouve une étape, où le numérateur de la fraction est multiple de 7 mais où l'on retrouve le résultat bien connu (espérons ;-) :
7/7 = 1 = 0,999999...
Le processus recommence aux étapes suivantes où l'on additionne simplement les chiffres en orange pour retrouver la période 142857.
8 x 142857 = 1142856 et 8/7 = 1,142857...
9 x 142857 = 1285713 et 9/7 = 1,285714...
10 x 142857 = 1428570 et 10/7 = 1,428571...
Comme on peut le voir, toutes les fractions de 7 admettent, en base 10 une période unique (de 7 - 1 = 6 chiffres), illustrée dans la figure ci-dessus par le microscope numérique.
Cette période est unique pour toutes les bases de forme 3 + 7n. (Si n= 1 la base est égale à 10).
Mais encore en base 10 pour les premiers suivants :
(on pourra constater qu'ils ne sont pas tous présents)
7, 17, 19, 23, 29, 47, 59, 61, 97, 109,...