Graphe des fractions de n/23 en base 20+23n
Le graphe est semblable pour les bases 20, 43, 66, 89, etc... et plus généralement pour toutes les bases de forme 20 + 23n . Pour le visualiser, on partage simultanément le cercle en 23 et 20 parties égales. (les points rouges)
Les "chiffres" de la période sont représentés en gris.
L'inverse de 20 étant (15) le plus petit, c'est le graphe de 15 + 23n qui répertorie les bases de forme 20 + 23n :
Pour des détails sur la génération des graphes cliquez ici.
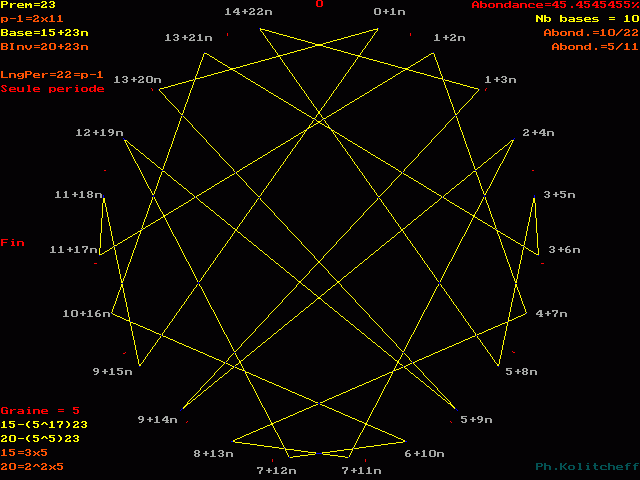
Les points du graphe (les facteurs de n) sont disposés dans l'ordre suivant en base 20+23n :
1-20-9-19-12-10-16-21-6-5-8===22-3-14-4-11-13-7-2-17-18-15
Et dans l'ordre inverse en base 15+23n :
1-15-18-17-2-7-13-11-4-14-3===22-8-5-6-21-16-10-12-19-9-20
Cela est normal si l'on songe que 20x15 admet 1 pour reste dans la division par 23, et qu'ils sont alors inverse dans Z23.
Pour les courageux qui voudraient vérifier, calculons 1/23 en base 15+23n (15, 38, 61, ...).
La période est la même pour tous les numérateurs, une seule ficelle suffit à les joindre tous, visitant ainsi les points de 1 à 22.