EUCLIDOSCOPE

PRESENTATION DU PROGRAMME

L'exécutable "MINUM" téléchargeable permet l'observation en un graphe# de toutes les fractions k/n
des nombres entiers k et n inférieurs à 3000, dans toutes les bases, fussent-elles infinies.

Prenons l’exemple du nombre 21 en base 10 et regardons comment il peut être représenté graphiquement lors de la division par 21 d’un nombre quelconque (que l’on appelle dividende).

Pour comprendre le fonctionnement du programme il est important d'imprimer le fichier PRESENTATION que vous venez de télécharger et de suivre pas à pas les indications. A moins que vous n'ayez le courage (ou l'opportunité) de suivre cette présenttion sur écran !

Au premier démarrage le programme (qui s’éteint en appuyant deux fois sur la touche < Esc>) affiche le nombre et la base fixés dans son fichier de configuration (Minum.ini aux rubriques Nombre=21 et Base=10 qui seront traités dans l’exemple ci-dessous).

Puis sur trois lignes en gris, viennent des calculs faisant intervenir la base inverse celle-ci reproduit la même figure en base 19 (il suffit d’appuyer sur <i> et revenir à la base 10 en appuyant une deuxième fois sur <i>) mais les graphes# sont parcouru en sens inverse. Enfin on trouve le comptage des périodes par exemple, deux périodes de 1 et deux périodes de 6. Celui-ci résume les graphe# ou l’on peut découvrir les détails pour tous les dividendes de 1/21 à 21/21 dans la table des dividendes primaires. 7/21 et 14/21 soit 1/3 et 2/3 ont une période de un chiffre représentées par un petit rond visible aux points 3+7n et 6+14n.

On trouve en haut à gauche à la première ligne, en orange, le nombre 21 dont on va découvrir les graphe# des dividendes.
A la deuxième, en jaune ; on trouve « non premier »  sinon, la décomposition en facteurs premier de p-1.
A la troisième, en orange , on trouve la base 10 pour simplifier.
A la quatrième on trouve la décomposition en facteurs premiers de la base soit pour 10, 5*2.

Puis sur trois lignes en gris, viennent des calculs faisant intervenir la base inverse celle-ci reproduit la même figure en base 19 (il suffit d’appuyer sur <i> et revenir à la base 10 en appuyant une deuxième fois sur <i>) mais les graphe# sont parcourus en sens inverse. Enfin, on trouve le comptage des périodes (par exemple, deux périodes de 1 et deux périodes de 6). Celui-ci résume les graphe# où l’on peut découvrir les détails pour tous les dividendes de 1/21 à 21/21 dans la table des dividendes primaires. 7/21 et 14/21 soit 1/3 et 2/3 ont une période de un chiffre représentées par un petit rond visible aux points 3+7n et 6+14n.

A droite se trouve la table des dividendes primaires. Ils sont ainsi nommés car cette table sert à effectuer le tri des dividendes en indexant la table sur le plus petit chiffre de la période. Elle ne peut pas bouger, notre première action sera de cliquer sur le 1 pour découvrir la période de 1/21 et la table de ses dividendes secondaires complètement à gauche. Cliquer sur un dividende secondaire permet d’effectuer à droite du tableau des dividendes secondaires et en deux colonnes les détails du calcul et dans la colonne de droite le résultat du calcul chiffrés par une formule de type b +(an).

Le programme compte dans la table de droite les périodes à un chiffre et les périodes primaires de 1/21, 3/21 et 5/21 en base 10, qui comportent chacune 6 chiffres sur toute leur longueur.

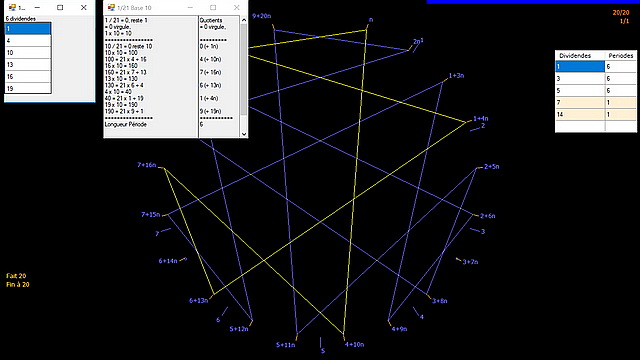
Si l’on n'a touché à rien, figure seulement un tableau à droite qui contient deux colonnes : celle du dividende à choisir et celle de la longueur de la période obtenue. En utilisant ce dividende 1 en base 10 on obtient les dividendes secondaires 4, 10, 13, 16 et 19 dont la même période comporte 6 chiffres. Et la période (0+1n), (4+10n), (7+16n), (6+13n), (1+4n), (9+19n) restant stable.

Choisissez donc le dividende « 1 » d’un double-clic de souris sur la colonne des dividendes. Auparavant si vous avez déjà modifié le nombre et la base, tapez « n21<Entrée> « et « b10<Entrée> » pour les initialiser conformément à cet exemple.

Nous avons isolé graphiquement par un savant coloriage (en jaune) le dividende voulu (1) appelé dividende principal, ainsi que les dividendes secondaires, 4, 10,13,16 et 19 qui apparaissent dans le tableau à gauche de votre écran. Tous ces dividendes secondaires partagent le même graphe de 1/21.

En résumé, un double-clic sur un dividende secondaire fera s’afficher les détails pour ce dividende secondaire.

Vous pouvez alors vous amuser à suivre dans la colonne résultat du calcul les formules des chiffres de la période choisie pour la retrouver sur le graphe. Ou encore taper sur la touche <i> pour passer à la base inverse de 10, soit la base 19 et retrouvant le même graphe, lire les formules à rebours du sens utilisé pour la base 10. Dans les deux cas, en base 10 et en base 19, en lisant la colonne des formules on verra de haut en bas et dans le même ordre les formules à retrouver sur le graphe de l’écran principal, disposées arbitrairement dans le sens des aiguilles d’une montre.

Si on a choisi le graphe de 1/21 en base 10 on obtient, en jaune, les 6 chiffres suivants: (0+1n), 4+10n),(7+16n),(6+13n),(1+4n),(9+19n). On retrouve la même période pour les dividendes secondaires 4/21, 10/21, 13/21, 16/21 et 19/21, qui génèrent le même graphe en décalant les chiffres d’un ou plusieurs crans. Le chiffre 9+19n étant caché par les détails du calcul, vous pouvez utiliser la souris pour changer la place des deux tableaux de gauche des détais des calcul et les dividendes secondaires car ils empiètent un petit peu sur la figure, et ça fait mal.

Pour  les deux tableaux de gauche vous pouvez les effacer avec la touche <*>. Une deuxième pression sur cette touche vous permettra, si vous voulez vous reposer sur une figure afin de vous interroger sur sa construction (période unique, les carrés, ceux de la touche <f>, les inverse, les pétales de lotus, etc.), d’effacer le tableau des dividendes primaires. Enfin une troisième pression sur <*> restaurera le tableau des dividendes primaires.

Il est temps maintenant pour nous d’essayer toutes ces combinaisons faisant continument varier le nombre avec les flèches curseur <Haut> et <Bas> ainsi que la base avec le flèches <Droite> et <Gauche>. Les deux tableaux de gauche devant être désactivés pour appuyer sur une touche. On tombera parfois malencontreusement sur le message « L’index et la longueur doivent faire référence à un emplacement situé dans la chaine. Nom du paramètre length », c’est une division par 0 ; on retourne au programme en appuyant sur <Entrée> ou <Esc>, et les résultats sont quand même justes ! Je suis désolé de ne pouvoir le corriger de par ma myopie galopante.

On peut aussi appuyer sur la touche <Alt> en même temps que <Bas>, <Haut>, <Droite> et <Gauche> pour n’obtenir que des périodes uniques pour des nombre exclusivement premiers. Attention toutefois à ne pas entrer un nombre trop grand, à partir de 4000 environ le programme se perd dans une boucle qui semble infinie. Il faut alors utiliser le vieux <Ctr><Alt><Suppr> et choisir le gestionnaire des tâches, trouver Minum.exe pour exécuter d’un click bouton droit et fin de tâche.

Plus rapidement vous pouvez, si vous le voulez, taper n7 <Entrée> pour constater que le graphe de 3/21 est similaire (aux formules près) au graphe de 1/7 ce qui est normal car 3/21 est égal à 1/7. Mais tapez plutôt n37<Entrée> pour observer les 12 triangles de n/37 en base 10. Il y a douze triangles de trois côtés et 3*12=36=nombre-1=37*-1=n-1. Cela veut dire que la totalité des (n -1) dividendes est visitée et la résonnance de 37 en base 10 est maximale ; cela est normal car il est premier. Vous pouvez alors calculer l’inverse (dont le graphe en tout point semblable à l’exception du sens de rotation des chiffres) de la base 10 c’est-à-dire le nombre qu’il faut multiplier par 10 pour que le résultat de la division par 37 donne 1. C’est-à-dire 26*10= 260 = 7*37+1.

Vous pouvez encore rester sur 21 (Tapez n21<Entrée>) puis sur Q, en double cliquant sur la première colonne (8 ou 13), Vous obtenez la liste des carrés pour le nombre 21, c’est à la dire les bases qui, multipliées par elles-mêmes, valent 1, et se représentent graphiquement d’une façon très simple. En fonction du nombre, il peut ne pas y avoir de solution à l’équation base élevée au carré égal un. Le programme affiche alors : « pas de carré trouvé ».

Essayez de calculer les 12 sortes de périodes de 4000 en base 21. On obtient 19 périodes à un chiffre, 8 de 200 chiffres, 8 de 40, 8 de 50 etc. douze en tout et même 2 périodes de 2.

Voilà, c’est terminé, vous savez utiliser l’Euclidoscope. Il me reste à me retirer en vous laissant méditer sur 211 en base 24 (n211<Entrée>b24<Entrée>).
Faites-vous des collections de vos meilleures trouvailles avant de les faire imprimer (tee-shirt, pin’s, nappe, vaisselle, dôme sur votre toit, toile de parachute, mandala, foulard, drap, etc. Envoyez-nous des photos de vos meilleures créations...

P.S : Perso, je vagabonde de 1000 à 3000 avec la touche <Alt>qui permet d’afficher exclusivement des périodes uniques, Puis j’appuie sur <S> presque à chaque fois.

            S’ensuit une collection d’images dans MesDocument (ou un dossier plus personnel).
On peut faire ce que l’on veut de cette Collection unique et personnalisable. Chaque couple Base/Nombre a une représentation unique, et personne pas même l’inventeur du dispositif ne saurait les retrouver à partir de leur seule image. Faites en un logo pour une société, personne n’arrivera à le reproduire. Ou un logo pour une association caritative, familles, groupe d’amis. Les représentations visuelles d’objets mathématiques sont libres de droit.

Vous pouvez ici télécharger une version TXT de ce document.