Graphe des fractions de n/67 en base 61+67n
Le graphe est semblable pour les bases 61, 128, 195, 262, etc... et plus généralement pour toutes les bases de forme 61 + 67n . Pour le visualiser, on partage simultanément le cercle en 67 et 61 parties égales.
L'inverse de 61 étant (11) le plus petit, c'est le graphe de 11 + 67n qui répertorie les bases de forme 61 + 67n :
Pour des détails sur la génération des graphes cliquez ici.
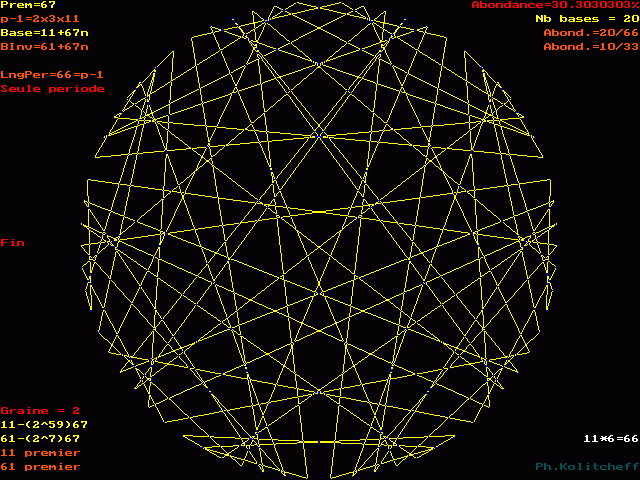
Les points du graphe (les chiffres de la période) sont disposés dans l'ordre suivant en base 61+67n :
1-61-36-52-23-63-24-57-60-42-16-38-40-28-33-3-49-41-22-2-55-5-37-46-59-48-47-53-17-32-9-13-56===66-6-31-15-44-4-43-10-7-25-51-29-27-39-34-64-18-26-45-65-12-62-30-21-8-19-20-14-50-35-58-54-11
Et dans l'ordre inverse en base 11+67n :
1-11-54-58-35-50-14-20-19-8-21-30-62-12-65-45-26-18-64-34-39-27-29-51-25-7-10-43-4-44-15-31-6===66-56-13-9-32-17-53-47-48-59-46-37-5-55-2-22-41-49-3-33-28-40-38-16-42-60-57-24-63-23-52-36-61
Cela est normal si l'on songe que 61x11 admet 1 pour reste dans la division par 67, et qu'ils sont alors inverse dans Z67.
Pour les courageux qui voudraient vérifier, calculons 1/67 en base 11+67n (11, 78, 145, ...).
La période est la même pour tous les numérateurs, une seule ficelle suffit à les joindre tous, visitant ainsi les points de 1 à 66.