L’invention nommée Euclidoscope permet une visualisation graphique de certaines propriétés d’un nombre N entier quelconque au travers une base B de calcul donnée de forme B+kN. Elle se fonde pour cela sur le partage d’un même cercle en N et B parties égales. N étant le nombre à visualiser et B la base servant à nommer ses chiffres, k étant un facteur variant de 0 à l’infini. Cette congruence modulo N peut être utilisée par des mathématiciens, amateurs ou professionnels, et révéler certaines relations structurelles propres à tous les nombres, leur « Densité » vis-à-vis d’une base et leur « Résonnance » vis-à-vis de tous les autres nombres ; cette dernière étant définie à l’aide de la moyenne de toutes les densités du Nombre calculée pour toutes les bases « chiffrant » celui-ci (la prononciation des chiffres de la base nomme le chiffre dans une base plus élevée que 10). Cette invention est maintenant au service des mathématiciens et/ou informaticiens pour l’élaboration de maints théorèmes et conjectures.
Une simple planche avec B+N clous disposés en cercle fournit une image approximative de ce que l’on peut obtenir en liant d’un « fil d’Arianne » les fractions de N pour tous les dividendes d de 1/N à N/N et par congruence, tous ceux de 0 à l’infini à condition que ce dividende ne soit pas multiple de N. On se servira abondement des lois associées aux congruences pour définir la « Densité » d’un Nombre dans une Base. Elle est relative pour un nombre et une base donnée à la somme des longueurs des périodes associées à B et tous les dividendes d de N dans cette Base.
La moyenne des densités obtenues pour N dans toutes les bases de 2 à N+1, est utilisée pour définir une quantité propre au Nombre considéré et est nommée « Résonnance du nombre ». C’est un nombre rationnel positif. Cette résonnance est maximale lorsque le nombre dispose d’une puissante famille de petits facteurs premiers comme 2 ou 3 résonnants alors avec les autres nombres admettant cette propriété. Elle est minimale lorsque le nombre est facteur de deux grands premiers, et nulle si le nombre est premier.
Les nombreuses applications sont celles attribuées aux nombres entiers notamment en musique, en cryptage et pourquoi pas en esthétique, physique, chimie ou résistance des matériaux et autres théorie des nombres, particulièrement dans l’enseignement.
Le graphe des périodes se répartit à la manière d’un engrenage sur les N parties du cercle, B servant à nommer les « Chiffres » de cette période. La somme (« nommée Densité ») des longueurs de toutes les périodes pour une base donnée conduit alors au calcul de la moyenne de ces sommes pour un nombre donné définissant la « Résonnance » de ce nombre. Elle est égale à 1 si le nombre est premier, celui-ci — égoïste — ne résonnant qu’avec 1 et lui-même.
Ces graphes issus des périodes obtenues (des dividendes)/(un diviseur) pour une base quelconque n’ont, à ce jour et à ma connaissance, que trop rarement été évoqués en mathématiques, à fortiori dans toutes les bases et pour tous les nombres, premiers ou non.
La figure 1 suivante donne un aperçu des graphes des nombres en base 0, 1, 2, 3, 4 et 5. (132 mod 131 = 1)
 |
 |
 |
 |
 |
 |
| Base 0+10k b=0 mod 131 |
131 base 132 b=1 mod 131 |
131 base 133 b=2 mod 131 |
131 base 134 b=3 mod 131 |
131 base 135 b=4 mod 131 |
131 base 136 |
| Figure 1 | |||||
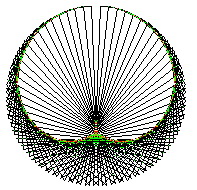
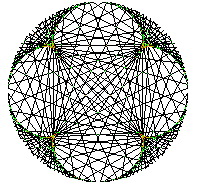
L’euclidosope se veut un outil graphique d’exploration des nombres dans une base qui leur donne forme. Il s’agit de partager le cercle en N et B parties égales, N étant le Nombre et B la Base. On calcule alors toutes les périodes Dividende/Nombre dans la Base voulue, les traçant sur le même cercle. Par exemple en base 10 on trouve les 5 périodes résultant de la division de d (d = Dividende entier) par 11 sur la figure (2) suivante avec d variant de 1 à l’infini.
En base 10 on partage en rouge le cercle en 10. Traçant les périodes des Dividendes de 11 en noir, le cercle est partagé en 10 et 11 parties égales. Pas de base Inverse.
Le premier trait du haut correspond à 1/11 = 0,090909… et 10/11 = 0,909090…
Le deuxième à 2/11 = 0,181818… et 9/11 = 0,818181…
Le troisième à 3/11 = 0,272727… et 8/11 = 0,727272…
Le quatrième à 4/11 = 0,363636… et 7/11 = 0,636363…
Le cinquième à 5/11 = 0,454545… et 6/11 = 0,545454…
Nous obtenons alors le graphe de tous les dividendes d/11 avec d variant de 1 à10. Si l’on met de côté les multiples de 11 (y compris 0x11) qui tombent toujours juste et n’ont pas de période, cela est suffisant. En effet, 11/11 = 1 et 12/11 = 1 + 1/11, 13/11 = 1 + 2/11 etc… Nous retrouvons 1, puis 2, etc. plus les mêmes périodes qu’entre 0 et 1, et nous avons donc représenté en une seule figure les périodes de tous les dividendes d/11 avec d variant de 0 à l’infini.
Parfois, le graphe peut se condenser en une seule et unique période comme dans le cas de d/7 en base 10, la longueur de la période est alors égale à N-1 (donc 6) et la figure peut se tracer sans lever le crayon (Figure 3). Cette propriété ne semble exister que pour des nombres premiers dépendant de la base de calcul.

Figure 3, d/7 en base 10
On partage alors le cercle en 7 et 10 parties égales et la période est la même pour tous les nombres non multiples de 7. 1/7 = 0,142857142857… 2/7 = 0,2857142857… 3/7 = 0,42857142857… etc.
Je ne connais pas de preuve que cette propriété d’unicité de la période concerne uniquement les nombres premiers, mais l’exemple de d/11 montre que la période n’est pas forcément unique si le nombre est premier, (N=11 admet 5 périodes de 2). En base 10, les premiers nombres à révéler cette propriété d’unicité de la période sont : 7, 17, 19, 23, 29, 47, 59, 61, 97, 109, etc. Ils sont tous premiers et probablement en nombre infini. Cette propriété d’unicité de la période se manifeste pour d’autres premiers en fonction de la base de calcul. Elle semble inexistante en base 4.
La période 142857 tirée de d/7 en base 10 admet d’autres propriétés. Si l’on pose 1 = 0,999999…
On trouve 999999 / 7 = 142857 ou 999999 – 142857 = 857142 et l’on retombe sur nos pieds. Bien plus étrange, 142+857 = 999 (ce qui garantit la symétrie de la figure) ou encore 143x999 = 142857. Etant relativement peu étudiées en mathématiques, on peut se demander si ces symétries se retrouvent pour toutes les périodes uniques ou non avec N premier ou non.
Si le cœur vous en dit vous pouvez vérifier ces résultats pour (Fig 4a) d/17= 0,0588235294117647… 0588235…etc. où l’on peut rapidement vérifier que 05882352 + 94117647 = 99999999.Ou encore (Fig4b) d/19 avec 052631578 + 947368421 = 999999999. On remarquera à la fin de cette période la suite des puissances de 2 : 1, 2, 4, 8 (16 ?) et plus exactement la somme de la série 20m avec m variant de 0 à l’infini. Nous y reviendrons, le lecteur intéressé pourra consulter le site des chrysodes.
 ...
...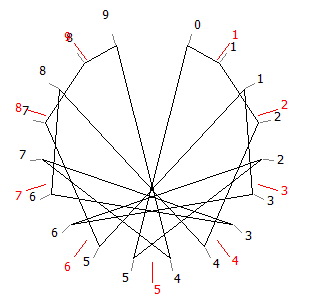
Figure 4a
x/17 en base 10
05882352 94117647
Figure 4b
x/19 en base 10
052631578 947368421
Pour le moment, examinons de plus près la période unique de d /17, les chiffres 1, 2, 4, 5, 7 et 8 y apparaissent tous deux fois. Cela est normal car si le cercle est partagé en 10 pour la base de calcul, il est partagé exactement en 17 parties égales et le nombre de chiffres de 0 à 9 est insuffisant pour parcourir les 16 points de la période. Du coup, ces 6 chiffres apparaissent en double. Dès lors, comment les distinguer? Les deux 1 sont bien placés entre 1 et 2. 2 entre 2 et 3, etc. Mais n’est-il pas arbitraire de choisir l’un plutôt que l’autre ?
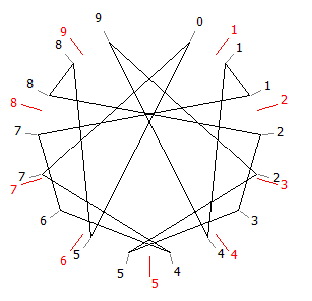
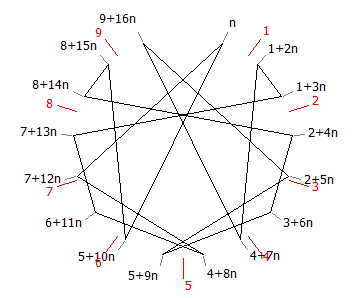
Pour tracer la figure, l’euclidoscope se sert de la loi des congruences (ici, modulo 17) et d’une représentation formulaire des chiffres de la période. L’astuce repose sur une remarque : le graphe est semblable pour toutes les bases de forme 10+17n (Figure 5a).
Et de fait pour les bases 10, 27, 44, 61 etc. n peut tendre vers l’infini et, par suite, la base peut être aussi grande qu’on veut, à condition d’être sous la forme 10+17n. Nous avons calculé les périodes en base de 2+17n à 16+17n de d/17 en base 10+17n. De plus, sachant qu’il est possible de calculer en base 0+17n où le résultat tombe toujours juste et qu’il est possible de calculer en base 1+17n si n est supérieur à 1, on peut calculer d/17 dans absolument toutes les bases 10 + 17n en obtenant le même graphe sans lever le crayon.
Pour les figures suivantes (Figure 5a et 5b) on considérera donc n=0 pour retrouver la base 10.
 ...
...
d/17 en base (10+17m)
05882352 94117647 si m=0
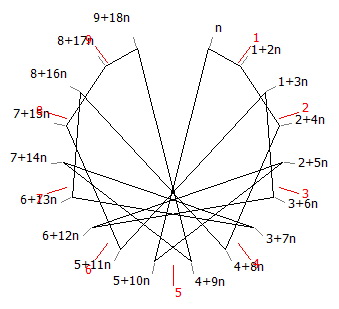
Figure 5b
d/19 en base (10+19m)
052631578 947368421 si m=0
Les figures suivantes (Figures 6a et 6b) illustrent les similitudes entre les bases 3+7n et 5+7n.
La loi des congruences impose que 1/7 en base 10 (10=3+7) admette les même formules qu’en base 3 et 1/7 en base 3 = 0,010212010212… (n=0) avec une période de 6 chiffres.
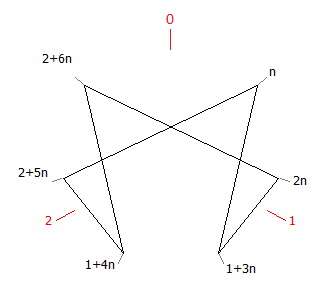
Et de manière générale 1/7 en base 3+7n : n, 1+3n, 2n, 2+6n, 1+4n, 2+5n (n=0),
où l’on retrouve à gauche la période 142857 de la base 10 si n=1 avec le même graphe.
On dit dans ce cas que 3 et 5 sont inverses modulo 7 (3x5 = 15 congru à 1 modulo 7, 3x5 admet 1 pour reste dans la division par 7).
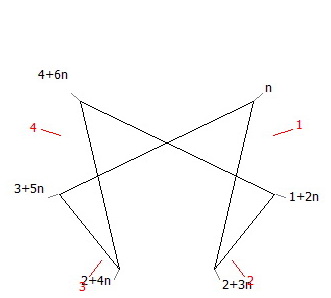
Avec à droite en base 5+7n la période 032412 de d/7 en base 5+7n qui est l’inverse de 3 (3x5 = 1 modulo 7) pour lequel la période est visitée à rebours du sens de 3+7n.
 .........
.........
La période 010212 de d/7 en base 3+7n avec n=0
La période 032412 de d/7 en base 5+7n avec n=0
Pour tous les nombres ci-dessus, on peut voir que tous les points (toutes les formules) sont visités par le graphe (le cercle en N parties égales). Nous verrons à l’usage qu’il en est de même pour tous les nombres premiers quelle que soit la base et le nombre de périodes associées. Mais cela est une exception. La majeure partie des nombres étant composée de facteurs premiers, leur graphe l’est aussi et leurs points ne sont pas forcément tous visités. Cela nous mène à une propriété du nombre par rapport à une base que l’on se propose d’appeler « Densité ». Elle se calcule à partir de la somme des longueurs de toutes les périodes (en fonction de tous les dividendes), divisée par le maximum théorique (N-1).
Par exemple, on cherche à établir la Densité de 7 en base 10.
7 en base 10 (ou en base 3+7n avec n=1) a une période de 6 chiffres et
une Densité de 6 / (7-1)=6/6 =1.
La Densité d’un nombre par rapport à une base est un rationnel compris entre 0 et 1.
Par exemple, 11 admettant 5 périodes de 2 chiffres a une Densité de (2 x 5) / (11-1) = 10/10 = 1 en base 10. On pourra constater empiriquement que les premiers ont une Densité de 1 (soit le maximum) pour toutes les bases, quel que soit le nombre de périodes. On pourrait dire, en quelque sorte, que les premiers sont « égoïstes » et ne résonnent qu’avec 1 et eux même. La situation est plus délicate avec les nombres composés. Ils n’admettent pas de périodes uniques, bien que leur Densité peut être égale à 1 dans une base donnée.
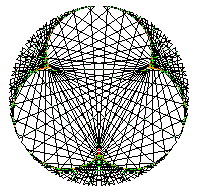
Un bon exemple de nombre composé (Figure 7) se trouve avec le graphe de d/34 en base 10.
1/34 = 0,02352941176470588 2352941176470588… est la période de d/17 en sautant un chiffre sur deux (Le premier 0 n’est pas inclus dans la période et on divise le cercle en 34 parties égales).
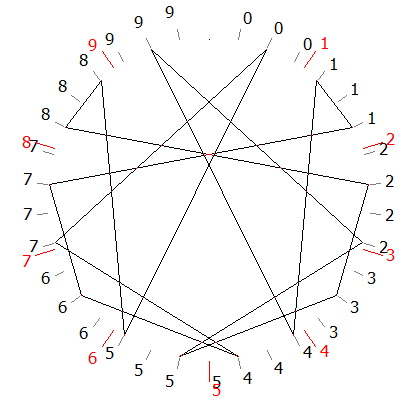
Figure 7
d/34 en base 10.
05882352 94117647
La période 2352 94117647 0588 de d/34 est la même que pour d/17.
La Longueur de la période est 16 avec un maximum théorique de 34-1. La Densité de 34 en base 10 est donc égale à (16/(34-1))=16/33 = 0,4848…
Nous verrons plus loin comment la moyenne des Densités (les longueurs de tous les dividendes variant de 0 à 1) calculée en Base 2 à N-1 nous mène à la notion de « Résonnance » d’un Nombre par rapport à tous les autres nombres. Nous savons déjà que la Densité d’un Premier (« égoïste ») est égale à 1 pour toutes les bases. En revanche, le Nombre peut être Non-Premier et avoir une Densité de 1. Par exemple d/21 avec 3 périodes de 6 et 2 périodes de 1 a une Densité de ((3x6) + (2x1))/(21-1) soit (18 + 2)/20 = 1.
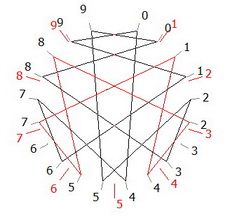
d/21 en base 10+21m avec deux périodes de 1 chiffre 3/21=0,33… et 6/21=0,66… correspondent à 3 et 6 qui semblent abandonnés sur ce graphe, mais qui comptent pour le calcul des Densités et de la résonnance sont figurés par des points dans le programme euclidoscope.

 ....
.... ....
....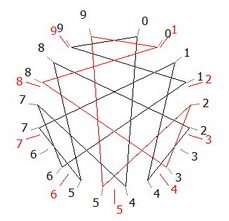
1, 4, 10, 13, 16, 19
047619
3, 6, 9, 12, 15, 18
142857
2, 5, 8, 11, 17, 20
095238
Où l’on peut voir les 3 fois 6 dividendes et dessous la période de 6 chiffres associée (en rouge). Le programme euclidoscope permet d’obtenir ces figures et toutes les étapes du calcul par un double-clic sur un dividende dans le tableau de droite (qui disparaît avec la touche [D].
En général, lorsque b=2n+1, les traits obtenus se rapprochent d’une sorte de sphère comme pour 47 en base 23 + 47n où, de plus, la période est unique (en base 23 et 45 son inverse).
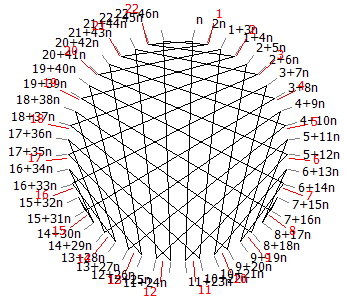
d/47 en base 23+47n, une seule période (sans lever le crayon)
Le programme Euclidoscope permet, à l’envie, d’afficher un nombre quelconque dans une base quelconque (inférieure à 100.000 actuellement) en pressant la touche [N] du clavier pour entrer le nombre et [B] pour entrer la base. Les touches curseurs [Droite] et [Gauche] incrémentent ou décrémentent la base, de même que [Haut] et [Bas] pour le nombre. Si de plus on appuie sur [Alt] on obtiendra le nombre premier (pour [N], ou la période unique (pour [B], immédiatement supérieur ou inférieur.
Une vue d’ensemble de toutes les densités d’un Nombre est disponible avec la touche [Entrée] qui permet de rassembler pour un Nombre et en une seule figure la longueur des périodes dans toutes les bases (de 2 à N-1) modulo N, N étant le Nombre. Cela permet de visualiser les graphes dans toutes les bases jusqu’à l’infini, en fonction de k avec une inconnue de forme (Bo +kN avec Bo < N, toutes les bases étant congrues à Bo modulo N). La même longueur de période — et la Densité de la figure — se retrouve dans toutes les bases plus k fois le Nombre, k variant de 0 à l’infini. Cette touche [Entrée] agit comme une bascule entre le graphe des densités d’un Nombre pour toutes ses bases et le graphe de ce nombre pour la base sélectionnée tournant avec les touches [Gauche] et [Droite].
Si la base est égale à 0+kNombre, le résultat tombe toujours juste, comme pour en base 10 : 10/ 10 = 1 et, 20/10 = 2. Il n’y a pas de période pour une base de forme 0+kn.
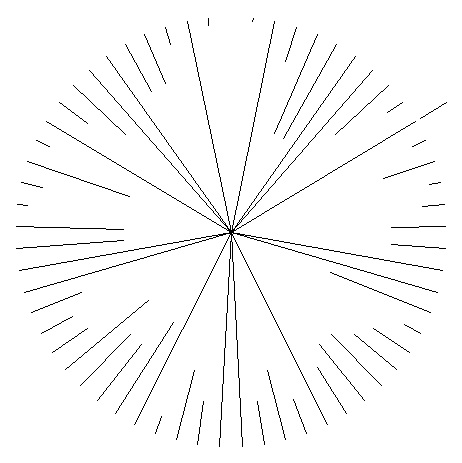
La base 1 peut être traitée car la longueur de la période est calculable en Base =Bo+kNombre (« Bo » étant la base inférieure au nombre, « Nombre » le nombre, « k » un coefficient un entier de 0 à l’infini) et donc en base 1 + kNombre si k n’est pas égal à 0. Les figures obtenues sont alors des points sur le cercle divisé en « Nombre » parties égales. La longueur de la période est 1 il y en a Nombre.
Voici quelques images qui représentent la Densité.
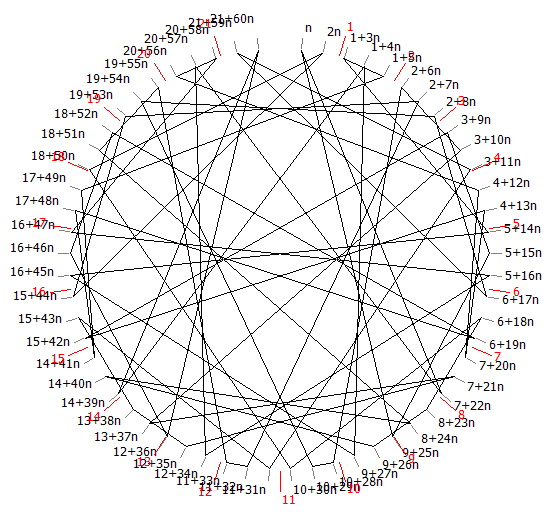
d/61 en base 22+61k
 ...
... 
On le voit, ces graphes permettent d’approcher les Nombres de manière visible. Les applications pratiques sont pour le moment principalement éducatives. Pour l’instant ils ne sont pas étudiés en Mathématiques mais on peut en voir l’utilité dans la théorie des nombres voire même dans des interprétations de relations obscures entre 238 et 92 (nombre de nucléons et nombre de protons dans l’Uranium). A vos théories, prêt ? Partez !
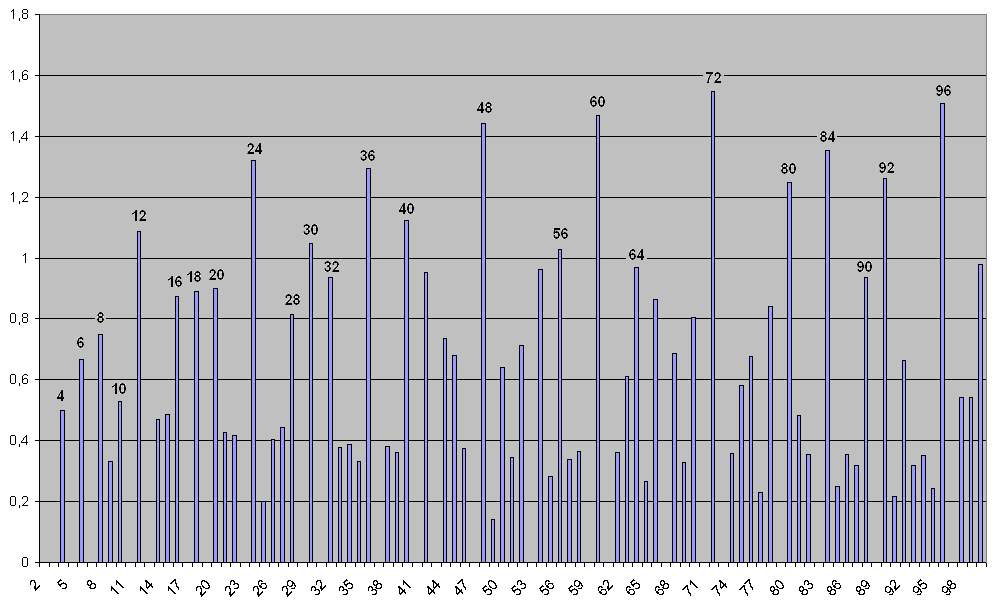
D’autres applications viennent à l’esprit. Par exemple, une autre mesure objective : réunir en une seule figure les Densités d’un Nombre (de 0 à 1) dans toutes les bases, afin d’estimer la résonnance de ce nombre avec tous ses semblables, le nombre étant entier, la moyenne de ses densités sera une somme de rationnels et donc située entre 0 et 1.
Il ne reste alors qu’a en calculer l’inverse et retirer 1 pour obtenir des valeurs facilement visualisables et égales à 0 lorsque le nombre est premier (la moyenne de 1 dans toutes les bases est égale à 1, à l’instar de la fonction Zéta de Riemann).
Par exemple toutes les Densités de 61(le curseur est placé sur la base 10, la base varie en pressant [Gauche] et [Droite].
L’Euclidoscope est un outil, ressemblant à un engrenage entre un nombre N de crans et une base B parcourant B crans. De la projection du nombre N dans la base B résulte un écran à 2 dimensions, représentant les relations entre le nombre et la base Bo+kN. (avec 1<Bo<N et k un entier de 0 à l’infini). Le nombre devient alors visible dans l’infini de toutes les bases.
Cet engrenage génère un graphe partageant le cercle en nombre de parties égales dans une base de 2 à B = N – 1) elle aussi partageant le même cercle divisé alors en B parties.
Et plus généralement en base (Bo+kN). Bo étant une base plus petite que N, et k un entier multiplicateur de N de 0 à l’infini, ces bases étant congrues modulo N, elles présentent toujours les mêmes graphe de 2 à l’infini.
La valeur toujours juste est attribué à B =kN/N. Et rien n’empêche.de calculer en base 1+k N si k non nul. En fait, Il permet de mesurer un Nombre N dans toutes les bases . Il défini la variable Densité pour une base. La moyenne de ces Densités pour toutes base inferieure au nombre, définissant la résonnance du nombre dans toutes les bases.
L’invention concerne la visualisation d’un nombre entier au travers d’une base de calcul. Elle se fonde pour cela sur le partage d’un même cercle en N et B parties égales. N étant le nombre à visualiser et B la base. On trace alors sur ce cercle les périodes obtenues pour tous les dividendes compris entre 0 et N ; et par congruence tous les dividendes de 0 à l’infini. Les graphes étant semblables pour toute la collection de bases B=Bo+kN. Avec Bo compris entre 0 et N.
Le graphe des périodes se répartit sur les N parties du cercle, B servant à nommer le « chiffre » de cette période. La somme des longueurs de toutes les périodes pour une base donnée conduit alors au calcul de la moyenne de ces sommes pour un nombre donné définissant la « Résonnance » de ce nombre.
Les nombreuses applications sont celles attribuées aux nombres entiers notamment en musique, en cryptage et pourquoi pas en esthétique, physique, chimie ou résistance des matériaux et autres théorie des ensembles.
Ces graphes issus des périodes des dividende/diviseur n’ont, à ce jour et à ma connaissance, que trop rarement été évoqué en mathématiques, à fortiori dans toutes les bases et pour tous les nombres, premier ou non.
Utilisant au mieux les lois de congruences on trouve non seulement que poser 0<d<N équivaut à calculer toutes les périodes de d variant de 0 à l’infini. De la même manière, on peut utiliser une représentation formulaire des chiffres de la période pour qu’ une base Bo inférieure à N telle que B= Bo+kN (k entier positif) conduise au même graphe avec k variant de 0 à l’infini.
La valeur «division de B/N = 0+kN/N toujours juste est attribué à B =kN/N.
On peut dans le monde des congruences de la base B modulo le nombreN.
Et la base est égale à Bo+kN. N étant le nombre, k un entier de 0 à l’infini.
On peut même calculer en base 1 + kN si k>0. Ce qui
Le théorème des conjectures
Nul ne sachant ce qui peut se produire car hormis 1 jamais une Résonnance d’un Nombre est égale à la Résonnance d’un autre Nombre (à démontre rigoureusement ?). Non , Il suffit de trouver un contre-exemple.

Hum ! je devrais faire des points.
Sur un graphe des résonances des 100 premiers nombres, on peut ne pas distinguer les premiers 2, 3, 5, 7, 11, 13, 17, 19, 23 etc. En effet, leur résonance est nulle.