EXEMPLE - Calcul de n/33.
La technique utilisé tout le long du site est semblable à celle illustée dans l'exemple suivant calculant les fractions de n/33.
Elle consiste à partager le cercle en
respectivement 10 (les petits points rouges)
et 33 parties égales.
On calcule alors les périodes de n/33 en base 10 puis en base 43 (10+33).
Cela est suffisant pour calculer de manière générale en
base 10+33n.
On réunit enfin en une seule figure toutes les périodes de n/33
en base 10+33n.
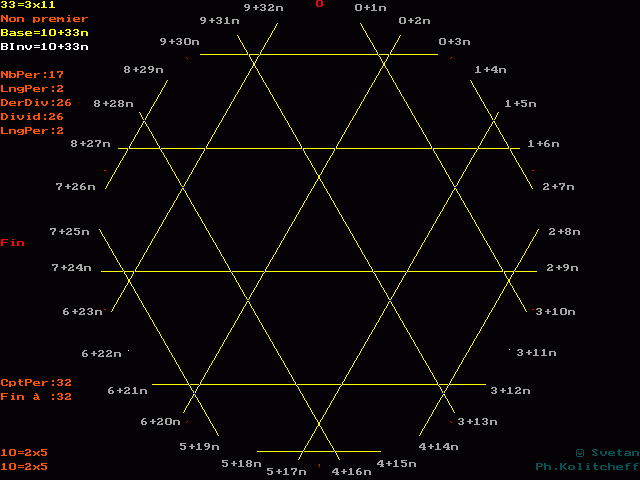
Constatons que ces périodes
se comportent comme une sorte de table de multiplication par 3.
1/33 = 0,03030303...
2/33 = 0,06060606...
3/33 = 0,09090909...
On retrouvera sans peine ces trois périodes et les suivantes dans la
figure ci-dessus.
La période 03
est représenté par le trait reliant 0+1n
et 3+10n (dans le cas particulier de la base
10, n est égal à 0).
Celle de 06 par le trait reliant 0+2n
et 6+20n.
Celle de 09 par le trait (0+3n,
9+30n), etc..
Viennent ensuite les périodes 12 (1+4n, 2+7n), 15 (1+5n, 5+17n), 18 (1+6n, 8+27n), 21 (2+7n, 1+4n), 24, etc.
Remarquons, chaque trait ayant deux bouts, que deux périodes leurs sont chaque fois associées. Ainsi, le trait (1+4n, 2+7n) représente à la fois la période de 4/33 = 0,1212... et la période de 7/33 = 0,2121...
Calcul de n/37:
Nous laisserons le soin au lecteur interressé de retrouver dans la figure suivante les 12 triangles formants les périodes de 1/37 :
On commence avec 1/37 = 0,027027027...
puis 2/37 = 0,054054054...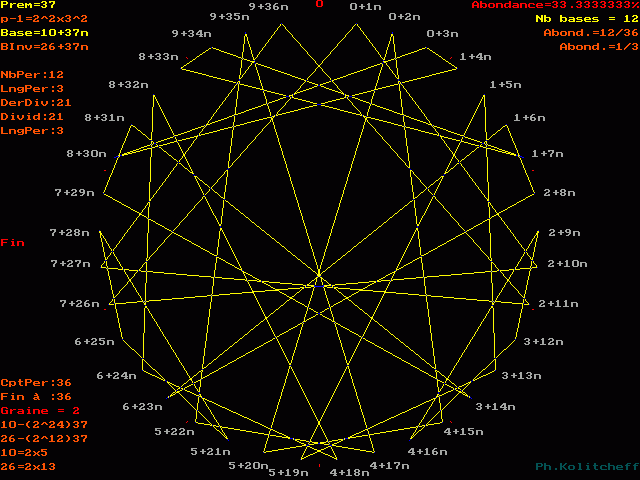
Remarquons que :
1/37 = 0,027027...
10/37 = 0,270270...
26/37 = 0,702702...
Admettent exactement la même période, ainsi que tous les autres triangles.
On retrouvera ici cette même technique appliquée aux nombres de 2 à 61.