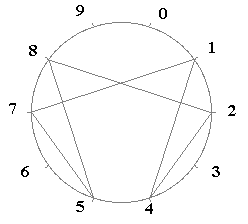
Euclidoscope
La division euclidienne est étudiée scolairement de la façon suivante en prenant l'exemple de la division de 1 par 7:
1.0000000...|
7.0
1.0...... | 0.142857.142857...
10...... |
1x7 = 7...... |
0.1
30..... |
4x7 = 28..... |
0.14
20.... |
2x7 = 14.... |
0.142
60... |
8x7 = 56...
| 0.1428
40..
|
5x7 = 35.. |
0.14285
50. |
7x7 = 49. |
0.142857...
1. |
10
|
|
Dans cette figure, les points à gauche du trait vertical représentent les zéros qui tombent du ciel comme par enchantement, mais qui correspondent en fait à une multiplication par 10, la base de calcul.
Ici le dividende initial est 1, mais nous voyons bien qu'il se transforme (car il est dépendant du reste de la division) en 10, 30, 20, 60, 40, 50 puis 10 encore et ainsi à l'infini. L'utilisation de la base 10 apparait ainsi clairement.
Cet exemple (1/7) n'a pas été choisi au hasard, il s'agit en effet du plus petit nombre qui génère en base 10 une période unique. Cette période admet entre autres propriétés une symétrie observable avec la figure suivante :

Les plus petits nombres admettant une période unique en base 10 sont tous premiers : 7, 17, 19, 23, 29, 47, 59, 61, 97, 109,...Mais on constatera que les premiers ne sont pas tous présent.
Par exemple 11 est premier, et lorsque l'on calcule n/ 11 en base 10, on constate qu'il existe cinq périodes qui se représentent ainsi :
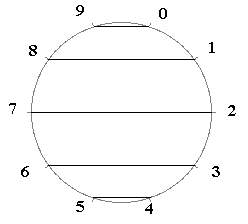
En effet,
1 / 11 = 0,09090909... est le trait du haut.
2 / 11 = 0,18181818... le trait d'en dessous
3 / 11 = 0,27272727...
4 / 11 = 0,36363636...
5 / 11 = 0,45454545...est le trait du bas.
Les périodes sont alors revisitées dans l'autre sens :
6 / 11 = 0,54545454...
7 / 11 = 0,63636363...
8 / 11 = 0,72727272...
9 / 11 = 0,81818181...
10 / 11 = 0,90909090...
Jusqu'au cas trivial :
11 / 11 = 0,99999999... = 1
Et le cycle se poursuit à l'infini avec:
12/11 = 1,09090909...
Où l'on retrouve la période de 1/11.
code de 1/11.