La résonance de tous les nombres
Le calcul de la résonance d'un nombre consiste à calculer pour un nombre N, la somme de la longueur de toutes ses périodes "dans toutes les bases", et à la normaliser.
En effet, pour obtenir un résultat équivalent pour tous les nombres qui permettra de les comparer, il faudra rapporter cette somme au maximum théorique possible, qui est égal à N-1 pour chacune des bases de calcul (le cas des premiers en est caractéristique, cette somme étant toujours égale à p-1 lorsque la base n'est pas un multiple de p).
Ici se pose un problème, que signifie "dans toutes les bases" ? La similarité obtenue pour les bases modulo N, nous autorise à ne calculer que pour les bases comprises entre 2 et N-1 pour étendre cette valeur aux bases 2+kN, 3+kN, 4+kN, etc.
Le nombre de bases à estimer variant de 2 à N-1 est alors égal à N-2. Et le maximum théorique possible pour la somme de la longueur de toutes les périodes de N, "dans toutes les bases" serait égal à (N - 1) x (N - 2).
On notera alors que si l'on ne peut calculer en base 1, il est toujours possible de calculer en base 1 + kN, lorsque k est différent de 0.
On pourrait penser, le résultat étant toujours le même (des périodes de un chiffre disposées autour du cercle des numérateurs), qu'inclure les bases de forme 1+kN n'influencera pas notablement le calcul. C'est une erreur. Outre le fait qu'inclure ces bases (de forme 1+kN) nous amène à un maximum théorique possible de (N - 1) x (N - 1) qui est un carré beaucoup plus élégant que (N - 1) x (N - 2), nous verrons plus loin quels autres avantages nous apporte cette subtilité.
Les divisions n/k tombant toujours juste pour les bases de forme 0+kN, la longueur de la période est nulle, et ces bases n'interviendront pas dans ce calcul (1/10 en base 10 vaut exactement 0.1, et plus généralement, il n'y a pas de période possible pour aucun 1/N en base N, 2N, 3N, etc.).
L'expression "dans toutes les bases" signifie donc :
Toutes les bases non multiples du nombre N à l'exception des bases 0 et 1.
ou encore
Toutes les bases de 2 à l'infini à l'exception des bases multiples de N.
Cette somme maximale étant atteinte pour tous les nombres premiers, la division de cette somme par (N - 1) x (N - 1) donnera toujours 1 lorsque le nombre est premier.
Il n'en est pas de même pour les autres nombres, et le calcul de cette valeur permettra d'estimer la résonance d'un nombre pour toutes les bases.
En voici les principaux résultats pour les nombres inférieurs à 100 (Fichier Excel),(Export txt):
Pour les nombres inférieurs à 1000 (Fichier Excel),(Export txt):
On notera ici la résonance de 720 utilisé pour les calculs du chapitre précédent.
Ainsi que des traits horizontaux au ordonnées 0,29 0,33 et 0,6 environ.
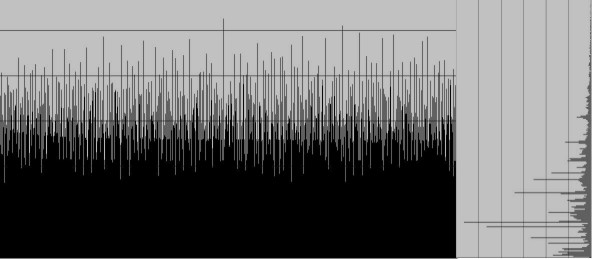
Enfin, pour les nombres inférieurs à 10000 (Fichier Excel),(Export txt):
Curieusement (?), des traits horizontaux se manifestent dans les vues ci-dessus. A l'ordonnée 0,33 et 0,29 pour le graphe des nombres inférieurs à 1000, ceux-ci seront noyés sous la masse dans le calcul des nombres inférieurs à 10000, pour lesquels on pourra tout de même observer que les nombres à l'ordonnée 1,06 et 1,29 sont étonnament nombreux.
Partons alors du graphe des nombres inférieurs à 10000, et partageons le en ligne horizontale en limitant à deux chiffres après la virgule la valeur de la résonance. On peut alors compter pour chacune des tranches obtenues le nombre de résonance présente.
Concrètement, créons une table R10000 avec un champ ResRed contenant l'arrondi de la résonance à deux chiffres après la virgule. Des outils de gestion de base de données, permettent alors à l'aide de la requête :
SELECT [ResRed], count(*) FROM R10000 GROUP BY [ResRed] ORDER BY [ResRed];
De compter les résonances présente sur toutes les tanches horizontales 0,01 0,02 0,03 0,04...jusqu'à 2,63.
La correspondance est donnée par la figure suivante où l'on observe le nombre d'occurence trouvé pour chacune des tranches.
Et où l'on voit mieux le comptage (Fichier Excel) ainsi :
La base de données R1000 (en réalité une simple table) est disponible sous ce lien, accessible à l'aide du bouton droit de la souris en choisissant l'option "Enregistrer la cible sous" lisible avec Access sous "Fenêtres" (enfin Windows quoi). L'utilisateur ne possédant pas Access, pourra trouver ici un export de cette table en mode texte.
Les deux pics principaux, situés à 0,29 et 0,33 correspondent respectivement aux nombres de forme 3xP ou 2xP, avec P premier. On peut les observer dans la figure suivante, où seules sont représentés les résonances (calculées jusqu'à 10000) des nombres multiples d'un premier et des facteurs suivants dans l'ordre de grandeur de la résonance (pas de quantité, 2 puis 3 sont les plus nombreux).
| Facteur du premier |
2^3*P
|
2*3*P
|
2^2*P
|
3^2*P
|
2*P
|
3*P
|
5*P
|
7*P
|
11*P
|
| Résonance |
0,78
|
0,72
|
0,6
|
0,42
|
0,33
|
0,29
|
0,19
|
0,14
|
0.09
|
| Graphe seul |
Tous ces graphes sur la même figure :
On peut dès lors observer l'étonnante régularité des valeurs obtenues lorsque l'on calcule la résonance des nombres K*P avec P premier et K un nombre constant. Un cap important semble être franchi à 0,33 environ (en bleu) qui correspond à la fois au pic représentant le plus grand nombre de résonance (Voir plus haut), et aux nombres de forme 2*P. En dessous, la constante K est un premier, au dessus, un nombre composé.
Si l'on trie les nombres par résonance croissante, on pourra observer leur décomposition en produit de facteurs dans les tableaux en liens dans le tableau suivant :
| Facteur du premier |
2^3*P
|
2*3*P
|
2^2*P
|
3^2*P
|
2*P
|
3*P
|
5*P
|
7*P
|
11*P
|
| Réson. 1000 | |||||||||
| Réson. 10000 |
Si vous n'avez pas de connexion haut débit, il est conseillé de n'utiliser que les liens de la deuxième ligne qui répertorient les nombres inférieurs à 1000. La troisième ligne répertorie les nombres inférieurs à 10000 et les fichiers sont alors beaucoup plus volumineux. Tout ces résultats sont bien sûr extraits de la table R10000.
On notera que les plus petites valeurs supérieures à 0 font résonner les carrés des premiers.