L'abondance est le quotient du nombre de périodes uniques pour un premier, rapportée à p-1.
En gros, on calcule le nombre de périodes uniques pour toutes les bases de 1 à p-1 et on divise par p-1.
Le pourcentage obtenu correspond aux calculs effectués en haut à droite de l'euclidoscope lorsque le nombre est premier (la touche <Alt>).

Le calcul de l'abondance des premiers permet de les classer "naturellement"

Les premiers, peu enclins à partager leurs facteurs (ils n'ont que 1 et eux-même) sont par nature égoïstes.

Si de plus, la base qui les manipule (on a 10 doigts) les fait jouer dans une période unique, ils prennent alors un caractère plus prononcé, en ce sens qu'ils ne résonnent pas alors avec des premiers plus petits.

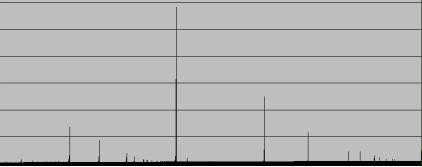
Pour illustrer cela, observons (à la loupe) la répartition de l'abondance des premiers inférieurs à 501089 (on est obligé de se limiter, cette figure correspond à 15 jours de calculs sur un Pentium II cadencé à 1 GHz). On a en abscisse l'abondance et en ordonnée la quantité de premiers.

On observe des pics :

La plus petite abondance est à gauche avec le premier record 120121 ayant une abondance minimale de 19,180819181...% se calculant à l'aide de 192 / 1001.

La plus grande abondance est à droite avec les premiers 3, 5, 17, 257, 65537 ayant tous une abondance maximale de 50%.

Le nombre de bases premières avec p-1 est alors maximal ainsi que le nombre de périodes uniques.

Note: 3, 5, 17, 257, 65537 (égaux respectivement à 2, 4, 16, 256, 65536, et donc 2, 2^2, 2^16, 2^32 plus 1) ne résonnent qu'avec 2, car leur décomposition en facteur premiers de p-1 est égale à une puissance de 2.En effet, étant tous de la forme (2^n) + 1, p-1 est alors premier avec la moitié des nombres entre 2 et p+1.

Si l'on calcule le logarithme du nombre de bases dans le spectre ci-dessus, on amplifie les petites différences (les abondances sont en abscisses).
On trouve alors la figure ci-dessous dans laquelle on peut isoler les abondances formant les pics les plus importants (en quantité de base):

20,77 - 22,85 - 26,66 - 28,56 - 30,29 - 30,75 - 33,33 - 34,27 - 36,34 - 36,90 - 38, 93 - 39,99 - 42,85 - 45,45 - 46,14 - 47,05 - 47,35 - 47,81 - 48,26 - 48,37 - 49,63 .

(Il est recommandé d'imprimer la figure ci-dessous pour bien observer les liens ci-dessus).

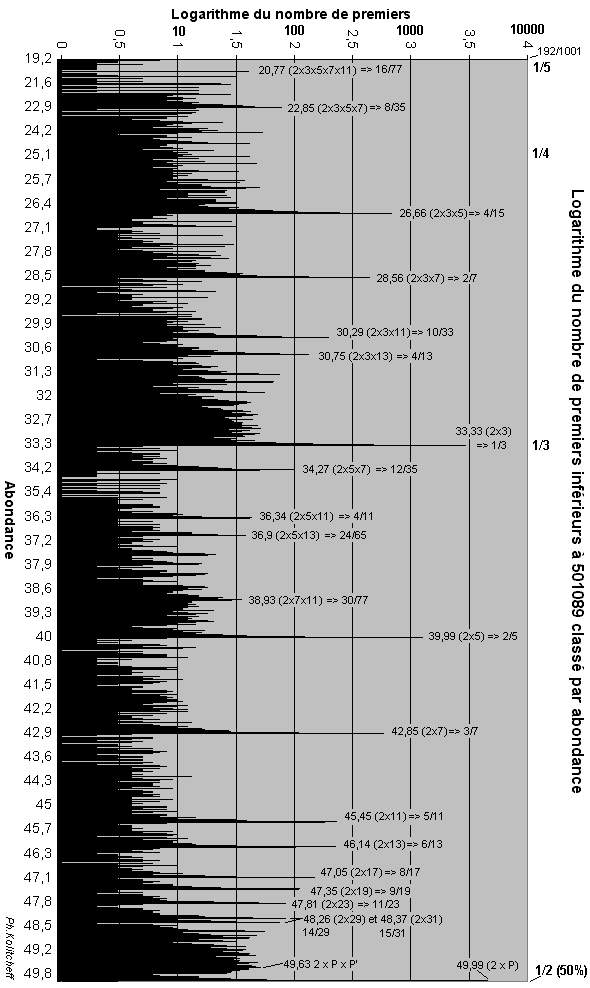
Jusqu' à arriver à l'abondance 49,8 (égale à 249/ 500) qui est un véritable butoir :

Au delà ne se trouvent que des premiers avec P-1 décomposable en 2*P'.

Où P' est premier aussi. Le plus petit d'entre eux est 503, son abondance est 49,800796813 (égale à 125/ 251) et dont p - 1 se décompose en 2 * 251.

Pour saisir tout le sel de cette figure, il faut consulter la base de données en téléchargement et en trier les champs par abondance et par premier.